Introduction

I am writing this post just to cement in my mind how to calculate a turn angle from one OSM segment to another. This is pretty basic geomertry but I tripped myself up last week and made a simple mistake that left me confused for way too long, as is tradition. At any rate, hoping to write this down both for myself and in case anyone else needs a dumbed down explanation of how to calculate if something is a right hand turn or a left hand turn and how much it is one or the other (a sharp right? a sharp left? for example).

Simple example set up

First we can create 2 example segments. Both will just have 2 coordinates (start node and end node). One leads to the next (so one way in OSM leading to another at an intersection). I will represent these as LineString objects and we can view them with GeoPandas:

import geopandas as gpd
from shapely.geometry import LineString, Polygon

seg1 = [[0, 0], [5, 9]]
seg2 = [[5, 9], [8, 8]]

seg1 = LineString(seg1)
seg2 = LineString(seg2)

gpd.GeoSeries([seg1, seg2]).plot(figsize=(3,3), color=["orange", "green"])

This will render the following:

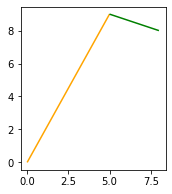
Calculating angles

First, we can determine the angle for each with a simple arctan calculation. We do this by generating a right triangle (as shown) for each and calculating the inverse of tangent (opposite over adjacent).

s1p = Polygon([
    [seg1.coords[1][0], seg1.coords[0][1]],
    [seg1.coords[1][0], seg1.coords[1][1]],
    [seg1.coords[0][0], seg1.coords[0][1]]
])

s2p = Polygon([
    [seg2.coords[1][0], seg2.coords[0][1]],
    [seg2.coords[1][0], seg2.coords[1][1]],
    [seg2.coords[0][0], seg2.coords[0][1]]
])

ax = gpd.GeoSeries([seg1, seg2]).plot(figsize=(3,3), color=["orange", "green"])
gpd.GeoSeries([s1p, s2p]).plot(ax=ax, color=["orange", "green"], alpha=0.2)

Now we can see the two triangles as determines using the x and y offsets:

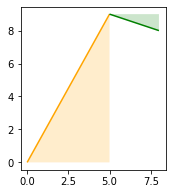
We can now calculate the angle for each triangle with the following:

import math

a1_radians = math.atan2(seg1.coords[1][1] - seg1.coords[0][1], seg1.coords[1][0] - seg1.coords[0][0])
a2_radians = math.atan2(seg2.coords[1][1] - seg2.coords[0][1], seg2.coords[1][0] - seg2.coords[0][0])

a1 = round(a1_radians * 180/math.pi, 2)
a2 = round(a2_radians * 180/math.pi, 2)

print("first angle (unadjusted)", a1)
print("second angle (unadjusted)", a2)

This prints the following:

• first angle (unadjusted) 60.95
• second angle (unadjusted) -18.43

We can also go ahead and normalize each of these to non-negative angles and consider this the bearing of each angle as a value between 0 and 360:

normalize = lambda x: round((x + 360) % 360, 2)
a1 = normalize(a1)
a2 = normalize(a2)

The values for each will be:

• first segment heading (adjusted) 60.95
• second segment heading (adjusted) 341.57

Calculate relative angle

Now that we have normalized heading for each segment on their own, we can simply determine the difference between the two, normalized between 0 and 360 as well, as the relative turn angle:

turn_angle = normalize(a1 - a2)
print("turn angle (degrees) from segment 1 to segment 2:", turn_angle)

We can assign angle types to these as well if we want to classify what kind of turn it is at each relative bearing. For example:

• values from 370 to 10 might be considered “forward”
• values from 10 to 40 might be a slight right
• values from 30 to 140 might be right
• values from 140 to 170 might be a sharp right
• values from 170 to 190 might be a u-turn
• …and similarly for the 190 to 370 as we did for the right turns, for the left turns